For my first internship, I worked at the Lawrence Livermore National Laboratory (LLNL) as a part of the High Performance Computing Cluster Engineering Academy (HPCCEA) program. As a part of this program, I got to experience how the computing division of one the world’s pioneering supercomputing centers was run. I worked on installing computing nodes, writing bash scripts and eventually using Ansible to automate the proces of bring up a new node. I was first exposed to and got pretty proficient in usingn the Linux command line interface, as when the nodes were first spun up, the command line was the only way to interface with it. Our scripts to automate the installation process can be found at the following Github Repository:
In addition to working on the cluster, I spent a majority of my time working on a project optimizing matrix multiplication algorithms for parallel computing environments. I worked with the naive and strassen algorithms, parallelizing them using the pthreads library and the openMP interface in C. In addition to distributing the workload to decrease the running time, I also used vector instructions specific to the Intel Sandy Bridge architecture to do SIMD dot products for additional speedup.
To characterize the behavior of both algorithms as the problem size increased, I read Intel’s Model Specific Registers (MSRs) to get low level information on each run’s execution–clock cycles, instructions executed, L1/L2 cache hits and misses. Using this data from the MSRs, I was able to use roofline analysis to determine at what input sizes the algorithms were compute bounds and when they became memory bound. I later use Intel’s PIN tools to count the times individual instructions were called to verify that no extraneous instructions were being issued.
For the naive matrix multiplication algorithm, the algorithm becomes increasingly more memory bound when the input size is greater than around 1000. In order to combat this, I would pull several values ahead into the cache to have faster memory reads. This significantly decreased the execution time.
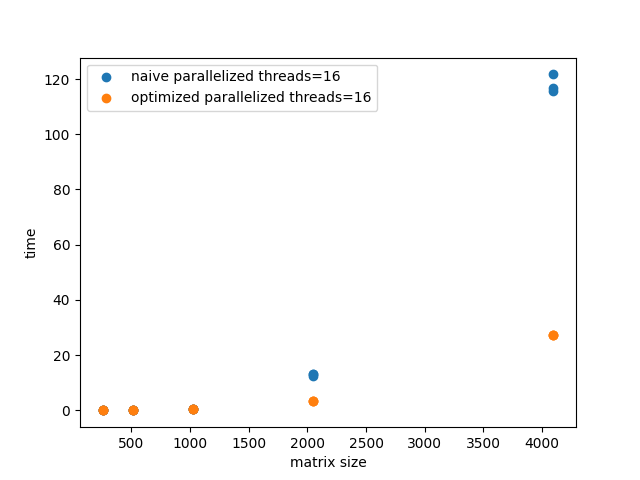
For the strassen algorithm for an nxn matrix, I used the n=2 input case as the base case for the recursion and then applied Intel Intrinsics vector instructions.
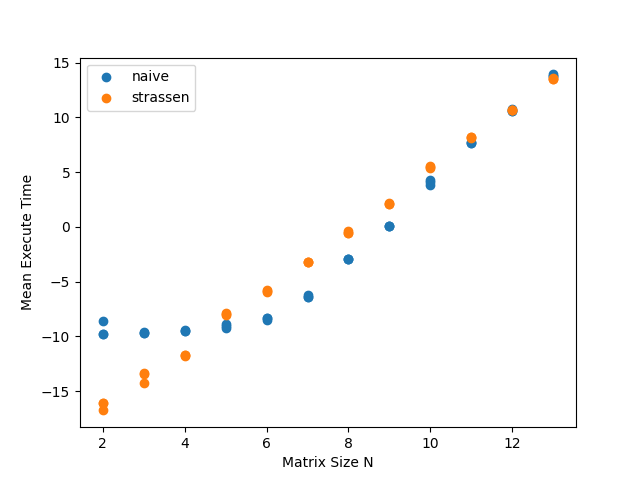
In the end, a comparison showed that the strassen algorithm only had a better performance than the naive algorithm when the input size was greater than 2^12 or 4096. This is because although the strassen algorithm has a better time complexity than the naive algorithm, the hidden constant in the Big-O is very large.
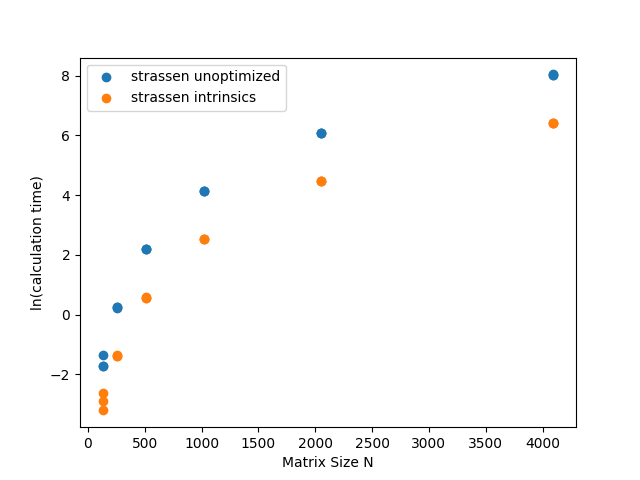
For a more through explanation of my findings, see the following Github repository for more graphs as well as the code to generate those results: